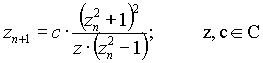Ein besonders interessantes Beispiel für selbstähnliche Funktionen ist folgende Gleichung, die [Peitgen und Richter] entnommen wurde, dort jedoch in einem anderen Zusammenhang behandelt erscheint:

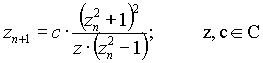Gl. 9-2

Diese im Gegensatz zur einfachen Parabel recht komplizierte Gleichung führt zu relativ langen Rechenzeiten, da für einen Iterationsschritt viele Operationen im komplexen Zahlenbereich durchzuführen sind und der Konvergenzbereich der Mandelbrotmenge relativ groß ist. Konvergenz erkennt das Programm bekanntlich durch das Erreichen der Maximalzahl an zulässigen Iterationen, was bei den hier angegebenen Beispielen immer der Maximalzahl an möglichen Farben (256) entspricht.

Aufgrund der Multiplikation mit der Konstanten c muß diese bei der Betrachtung einer Juliamenge ungleich Null sein, da sonst für jeden z-Startwert die Triviallösung z=0 folgt. Gleiches gilt für die Mandelbrotmenge, wo der Startwert z₀ ebenfalls ungleich Null bzw sein muß, da sonst der Nenner ebenfalls gleich Null wird, was zu einer unzulässigen mathematischen Operation führt.

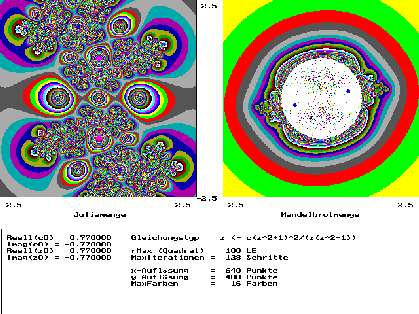
Abb. -1 Gegenüberstellung von Julia- und Mandelbrotmenge

Abb. 9-1 stellt sowohl die Mandelbrot- als auch die korrespondierende Juliamenge der angegeben Gleichung dar, wobei als Startwert bzw. Konstante hier und für die anderen Abbildungen der Wert

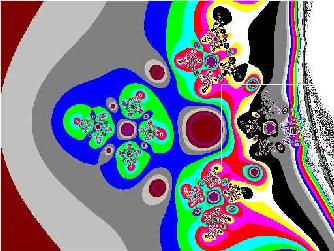
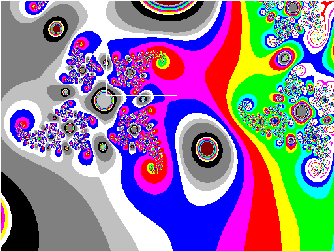
gewählt wurde. Mandelbrot- und Juliamenge zeigen auf den ersten Blick wenig Gemeinsamkeiten. Vergleicht man die folgenden Abbildungen, die sämtlich Ausschnitte der Mandelbrotmenge darstellen, so fällt auf, daß eins der Grundmotive immer wieder auftaucht, die linksdrehende Schnecke, die natürlich wieder selbstähnlich ist. Die linksdrehenden Schnecken sind ein einheitliches Motiv und ergeben sich wahrscheinlich aufgrund der Definition der Multiplikation zweier komplexer Zahlen, da hier der Winkel zwischen den beiden komplexen Zeigern links herum als positiv betrachtet wird. Diese Selbstähnlichkeit wird besonders durch Abb. 9-2e und Abb. 9-2f verdeutlicht. Sie stellen beide einen Teil aus der "Kinnschnecke" dar. Beide sind nahezu identisch, obwohl die eine Abbildung eine Vergrößerung der anderen ist. Dieser Vorgang ließe sich theoretisch unendlich oft wiederholen. Warum alle Schnecken linksdrehend sind, läßt sich wahrscheinlich auf die Definition der komplexen Zahlen zurückführen, die in der Darstellung der Polarkooordinaten auf die positive, linksdrehende Definition des Winkels bezug nehmen.

Tabelle -1 Zusammenstellung der Intervallgrößen für Abb. 9-2

Auch das Motiv des Apfelmännchens läßt sich aus dem Ausgangsbild der Juliamenge erahnen. Um diese Ähnlichkeit zu erreichen, ist es notwendig, die Iterationstiefe auf mindestens 1000 zu setzen, was natürlich zu extremen Rechenzeiten führt. Mehreren Abbildungen können als Motiv Köpfe verschiedener Art entnommen werden, wobei sich das Titelbild als Ausschnitt durch vertikale Spiegelung der Abb. 9-2d ergibt.